Optimizers in Neural Networks (very brief and on point)

Pratik Tiwari

6 min readFeb 4, 2021

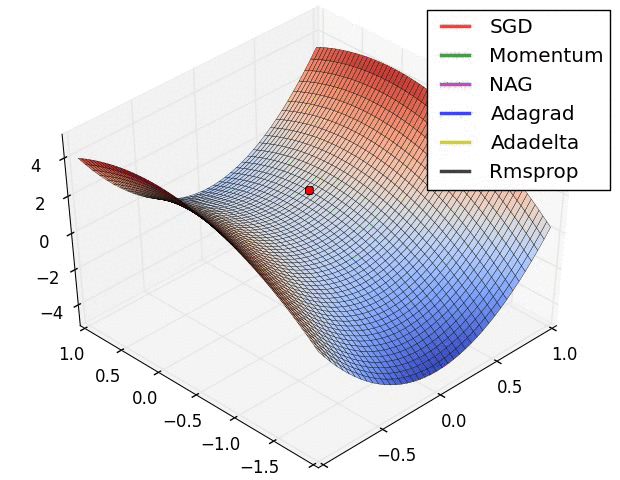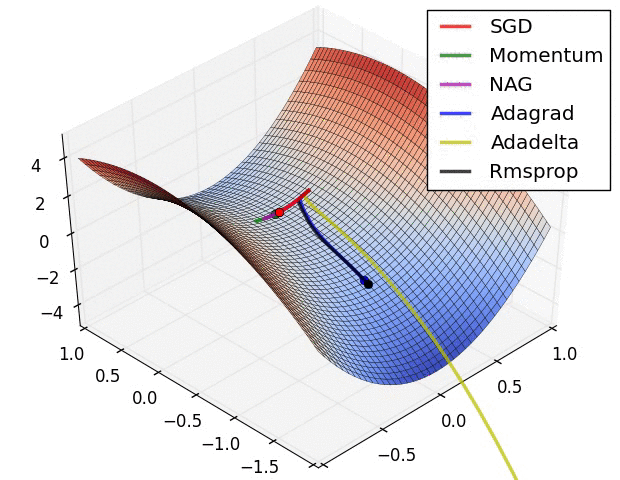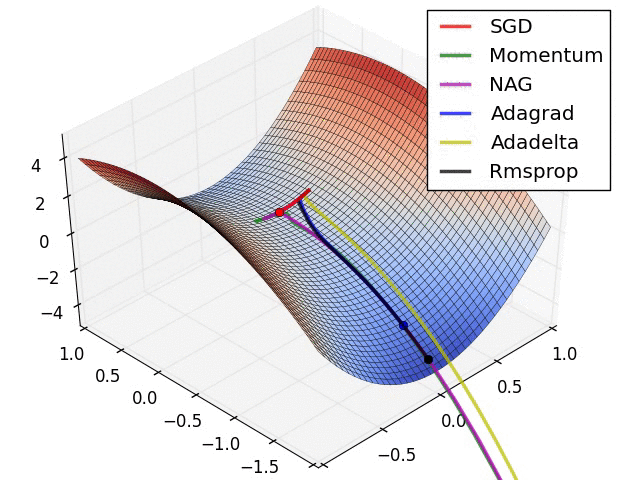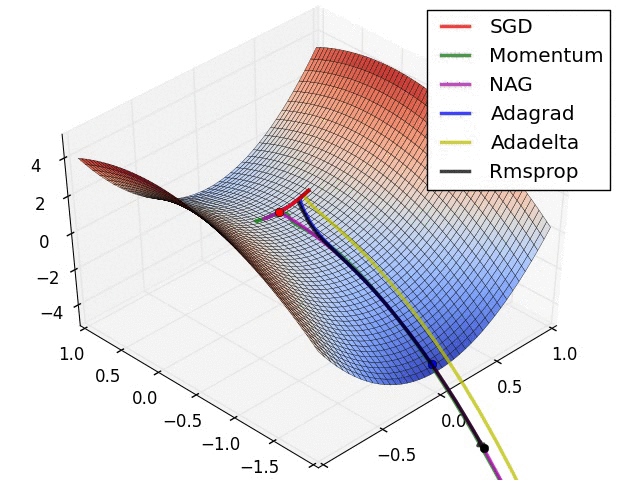
Optimizers: They optimize the learning rate in back propagation

Batch Gradient Descent

If the have to use online (continuously coming data) learning or the data is huge we dont use batch GD
In case we are sending all the data at once.

stochastic Gradient Descent

WHY SGD WAS USED?

Suppose we have like 1 million record to train through a deep neural network if we train this many records it will do back propagation for each record and update the weights this may take like a really huge time and take an ample amount of computational resource hence SGD was used.
In case we dont have all the data but we send it in multiple bunch.
It has a range in structured data Example. 256–10000 (data (rows))
It has more than 1 minima as the NN will find minima for each batch of data.
Less memory is needed as all the data is not loaded at once.

Mini Batch Gradient Descent

If the batch size 50–256 record so the batch size is much much less than BGD or SGD.
It has more than 1 minima as the NN will find minima for each batch of data.
Variance is experienced very less as the data size size is very less.
The learning will not be a smooth learning as the NN doesnt know the whole data but just a batch of data hence the learning rate will change likewise and will create a an un even pattern in attaining minima

PROBLEM WITH VANILLA IMPLEMENTATION

Here the learning rate is constant even after back propogation we have understanding of the weights and biases we keep the learning rate as constant which not always a good thing to do.
We are not considering the weights which are before n-1 weight to come to the resultant(last) weight we have come from a n-2 weight as this is not sufficient and we should also take into account the weights before n-1 this implementations does not allow that.
To counter part when we re taking the weights we should take the change in weights of the weights before n-1 not actual weights but change in weight.

ADEM Adaptive Moment Estimation Optimizer

To solve the problem of constant eta and eta not be ing able to learn itself while BP.

Here if the only changing thing is vt if vt decrease the eta increases which is what we want.

In this it takes in account the previous weight to calculate the new weights.

Basically it smoothens the effect of rapid change and noise in SGD and mini batch SGD.

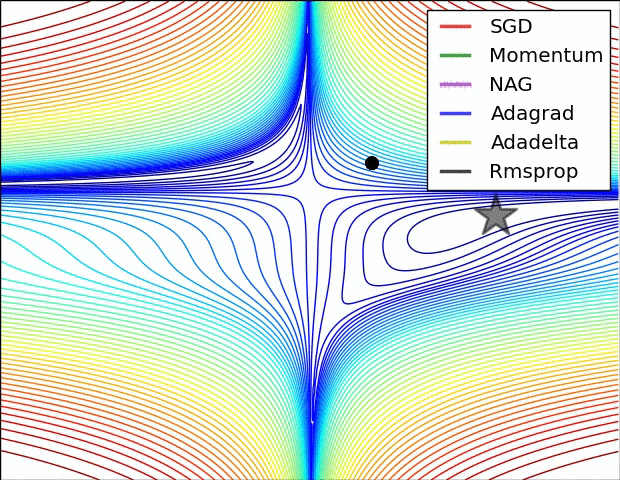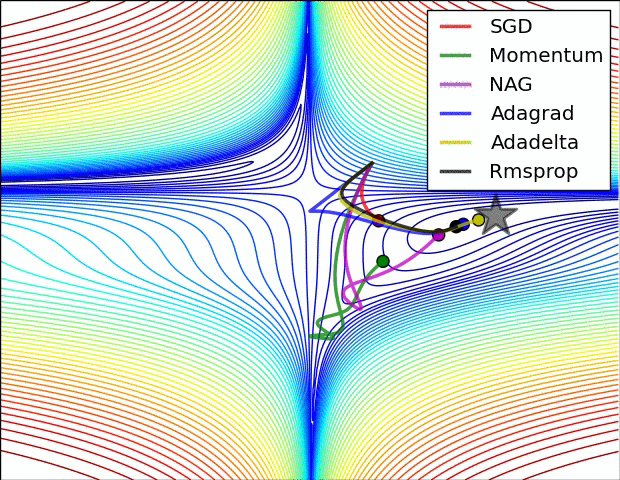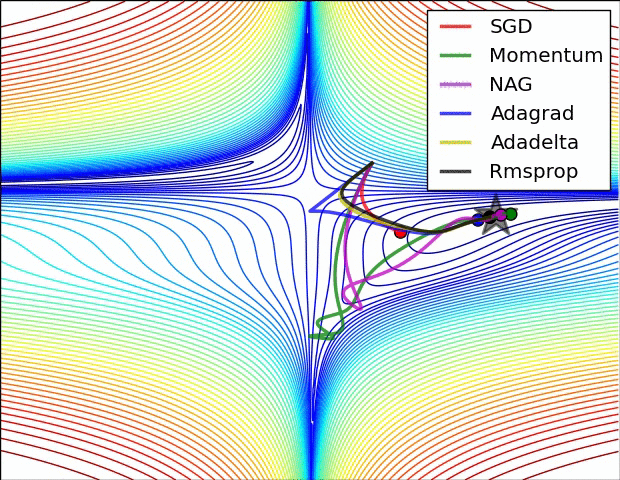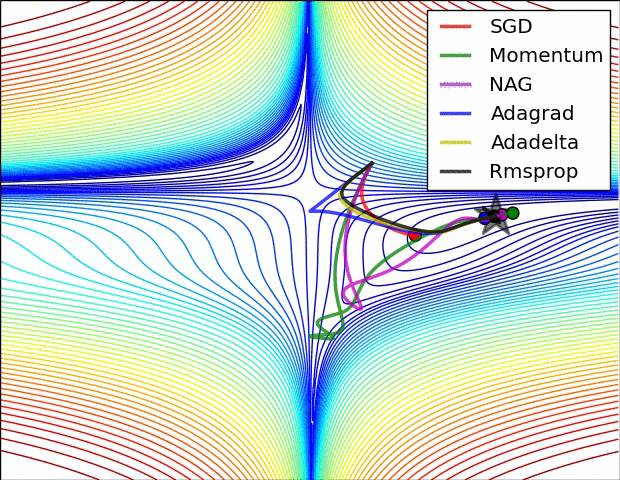
ADAGARD — Adaptive Gradient Descent

The concept is that while the GD is trying to attain the minim, what if we dynamically change the learning rate. A the num of iteration is increasing we decrease the learning rate of the GD.

$θt+1=θt−η/√Gt+ϵ⊙gt$ → where θ can be Weights and Bias
$Gt = (i=1) -> (i=t) Σ (dL/dW)²$

Here as the GT that is the increasing and the sum of the Gt as the time increases. When it becomes a big number when something divided by a big number is also a small value hence in each iteration the value decreases and hence the learning rate also decreases.
One Disadvantage if there is very deep neural net Gt will become a very big number and the learning rate will become very small hence there will not be any difference in the previous and new weights and biases and hence this is a problem hence the vanishing gradient problem.
Here ϵ is a small +ve number because if the Gt is zero we need a small number to no make the learning rate 0.
Adagrad is an algorithm for gradient-based optimization which adapts the learning rate to the parameters, using low learning rates for parameters associated with frequently occurring features, and using high learning rates for parameters associated with infrequent features.
So, it is well-suited for dealing with sparse data.
But the same update rate may not be suitable for all parameters. For example, some parameters may have reached the stage where only fine-tuning is needed, but some parameters need to be adjusted a lot due to the small number of corresponding samples.
Adagrad proposed this problem, an algorithm that adaptively assigns different learning rates to various parameters among them. The implication is that for each parameter, as its total distance updated increases, its learning rate also slows.
GloVe word embedding uses adagrad where infrequent words required a greater update and frequent words require smaller updates.
Adagrad eliminates the need to manually tune the learning rate.

ADADELTA / RMSE PROP

There are three problems with the Adagrad algorithm

The learning rate is monotonically decreasing.
The learning rate in the late training period is very small.
It requires manually setting a global initial learning rate

Adadelta is an extension of Adagrad and it also tries to reduce Adagrad’s aggressive, monotonically reducing the learning rate.
It does this by restricting the window of the past accumulated gradient to some fixed size of w. Running average at time t then depends on the previous average and the current gradient.
In Adadelta we do not need to set the default learning rate as we take the ratio of the running average of the previous time steps to the current gradient.

Here in case of ADADELTA here SDw will not explode because as we see in the equation of SDw it is getting multiplied with a 1-B(betta) where B is takken around 0.9–0.95 hence it will become a small value if something is divided by a small value it will not be a small value and hence we wont see vanishing gradient problem as the weights will change.

Adam — Adaptive moment estimation = Momentum(Smoothening) + RmsProp(No VG problem)

SO here we can see ADAM is best because it takes in advantage the momentum that is smoothening effect and also the Rmsprop that is the No Vanishing gradient problem

Here VDw = Momentum and SDw = Rmsprop

How to choose optimizers?

If the data is sparse, use the self-applicable methods, namely Adagrad, Adadelta, RMSprop, Adam.
RMSprop, Adadelta, Adam have similar effects in many cases.
Adam just added bias-correction and momentum on the basis of RMSprop,
As the gradient becomes sparse, Adam will perform better than RMSprop.

Overall, Adam is the best choice.

SGD is used in many papers, without momentum, etc. Although SGD can reach a minimum value, it takes longer than other algorithms and may be trapped in the saddle point.